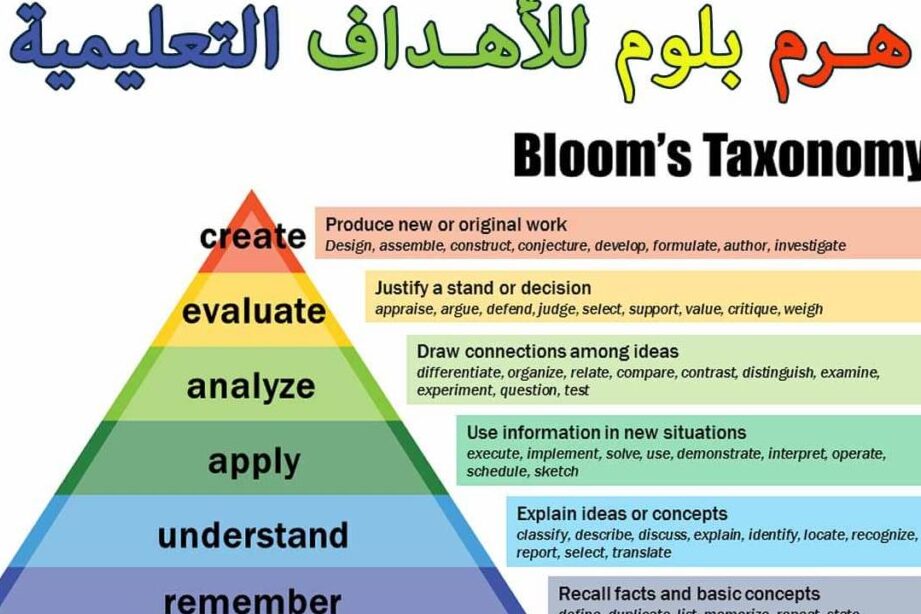
في عالم التعليم، تعتبر مستويات بلوم المعرفية من الأدوات الأساسية لفهم كيفية تطوير التفكير النقدي والمهارات الرياضية. لكن هل تساءلتم يومًا كيف يمكن تطبيق هذه المستويات في مادة الرياضيات؟ في هذا المقال، سنستكشف أمثلة على مستويات بلوم المعرفية في الرياضيات، حيث نقدم رؤى واضحة حول كيفية تحسين تعلم الطلاب وتعزيز فهمهم.
سنبدأ بالتعرف على كل مستوى من مستويات بلوم وكيف يمكن استخدامه في تدريس الرياضيات. سنتناول استراتيجيات فعالة تساعد المعلمين والطلاب على الوصول إلى مستويات أعلى من التفكير. من خلال هذه الأمثلة، نهدف إلى إلهامكم لتطبيق هذه المفاهيم في الفصول الدراسية الخاصة بكم. دعونا نبدأ رحلتنا في عالم الرياضيات ونكتشف كيف يمكن لمستويات بلوم أن تُحدث فرقًا حقيقيًا في تعلمنا.
أمثلة على مستويات بلوم المعرفية في الرياضيات
نركز هنا على مستويات بلوم المعرفية ونقدم أمثلة توضح كيفية تطبيقها في مادة الرياضيات. تتضمن هذه المستويات:
من خلال هذه الأمثلة، نلاحظ كيفية تحقيق مستويات بلوم في تعليم الرياضيات، مما يعزز التفكير النقدي لدى الطلاب. كما تجسد كل مستوى مهارات محددة تعود بالنفع على الفهم الشامل لمادة الرياضيات.
المستوى الأول: المعرفة
يمثل المستوى الأول من مستويات بلوم المعرفية أساس المعرفة في الرياضيات. يتمحور هذا المستوى حول استرجاع المعلومات، وتحديد المفاهيم الأساسية، وتذكر القوانين الرياضية.
تعريف المعرفة
المعرفة تعني فهم المعلومات والحقائق الأساسية المتعلقة بمادة الرياضيات. يمكن أن تشمل التعريفات، القوانين، والمبادئ الأساسية. في هذا المستوى، يتوقع من الطلاب التعرف على أنواع مختلفة من الأرقام أو العمليات، مثل الأعداد الصحيحة أو الجمع والطرح.
أمثلة على تطبيق المعرفة في الرياضيات
نقدم هنا بعض الأمثلة ذات الصلة بتطبيق المعرفة:
تمثل هذه الأمثلة التطبيقات الأساسية التي تشكل قاعدة متينة للمعرفة الرياضية. نساهم بذلك في تعزيز الفهم العميق للمفاهيم الرياضية، مما يساعد الطلاب في مراحل تعليمية لاحقة.
المستوى الثاني: الفهم
يمثل المستوى الثاني من مستويات بلوم المعرفية العنصر الأساسي لفهم المفاهيم الرياضية وتطبيقها بشكل فعّال. يمكننا تعريف الفهم بأنه القدرة على تفسير ومعالجة المعلومات الرياضية وتحويلها إلى رؤى ذات معنى.
تعريف الفهم
يتضمن الفهم القدرة على تحديد المعاني وتحليل المفاهيم الأساسية واستخدامها في سياقات مختلفة. تعتمد هذه المهارة على استيعاب المعلومات بعمق، مما يساعد الطلاب على إدراك العلاقات الرياضية وتطبيق القوانين بكفاءة. من خلال الفهم الجيد، يمكنهم الربط بين المفاهيم النظرية والتطبيق العملي.
أمثلة على تطبيق الفهم في الرياضيات
نستعرض هنا بعض الأمثلة التي توضح كيفية تطبيق مفهوم الفهم في مادة الرياضيات:
بهذه الأمثلة، نرسم صورة واضحة لكيفية إمكانية تعزيز الفهم في الرياضيات، مما يساعد الطلاب على التطور والتحسين في مهاراتهم النقدية.
المستوى الثالث: التطبيق
يمثل مستوى التطبيق في مستويات بلوم المعرفية نقل المعرفة والفهم إلى سياقات جديدة. يتطلب هذا المستوى استخدام المفاهيم والمهارات الرياضية لحل المشكلات أو تنفيذ العمليات.
تعريف التطبيق
يمثل التطبيق قدرة الطلاب على استخدام المعرفة الرياضية في مواقف عملية. في هذا المستوى، يتمكن الطلاب من تطبيق القوانين والمفاهيم التي تعلموها لحل مسائل رياضية معينة. يشمل ذلك استخدام الرياضيات في مجالات متنوعة، مثل العلوم والهندسة والاقتصاد.
أمثلة على تطبيقات رياضية
تتضمن أمثلة تطبيقية متنوعة تظهر كيفية استخدام الطلاب للمعرفة الرياضية بشكل فعّال:
- حل المعادلات الرياضية التي تتطلب استخدام القوانين الأساسية مثل قانون فيثاغورس.
- تطبيق مفاهيم النسب والتناسب في حل مسائل عن النسب المالية والمعدلات.
- استخدام العمليات الرياضية في حساب المسافات والزمن، مثل حساب سرعة سيارة.
- تحليل البيانات الإحصائية باستخدام المتوسطات والانحرافات المعيارية.
- رسم الأشكال الهندسية باستخدام أدوات الهندسة، مثل المسطرة والفينومتر.
- حل المشكلات الهندسية المتعلقة بحساب المساحات والأحجام مثل مساحة الدائرة أو حجم المكعب.
تظهر هذه الأمثلة كيف يُمكن للطلاب توظيف المهارات والمعرفة الرياضية في حل المسائل الحياتية، مما يسهم في تنمية التفكير النقدي والقدرة على التحليل.
المستوى الرابع: التحليل
يعتبر التحليل خطوة مهمة في مستويات بلوم المعرفية، حيث يتطلب القدرة على فهم المعلومات وتفكيكها إلى مكوناتها الأساسية. يمكننا من خلال التحليل تقييم البيانات والعمليات وتحديد العلاقات بين الأفكار.
تعريف التحليل
التحليل يعني تفكيك المعلومات أو المسائل المعقدة إلى أجزاء أصغر لتحليل مضمونها. يتضمن التحليل فهم كيفية ارتباط هذه الأجزاء ببعضها، مما يسهل عملية تقييم المعلومات ومعرفة الآثار المحتملة. من خلال هذا المستوى، نستطيع التفكير في بدائل أو حلول مختلفة لأي مسألة.
أمثلة على تحليل المسائل الرياضية
عند تطبيق التحليل في الرياضيات، نجد أن هناك العديد من الأساليب والممارسات المفيدة. إليكم بعض الأمثلة:
تساعد هذه الأمثلة على تطوير مهارات التفكير النقدي لدى الطلاب، مما يعزز قدرتهم على اتخاذ القرارات المستنيرة في الرياضيات.
المستوى الخامس: التركيب
يمثل مستوى التركيب من مستويات بلوم المعرفية القدرة على الجمع بين المعلومات والأفكار لإنشاء كائن جديد أو صياغة حلول مبتكرة. يتطلب هذا المستوى تفكيرًا نقديًا، حيث يمكن للطلاب تجميع عناصر مختلفة بشكل فعّال.
تعريف التركيب
يُعَرّف التركيب بأنه عملية إنشاء تركيبات جديدة من خلال مزج المعلومات بطريقة مبتكرة. يتضمن هذا المستوى تطوير أفكار أو استراتيجيات أو نماذج رياضية فريدة من نوعها. التركيب يعكس عمق الفهم والمعرفة المترابطة، حيث تمكن الطلاب من تجميع الحلول بطريقة فعّالة تساهم في تعزيز الإبداع.
أمثلة على التركيب في الرياضيات
تتعدد الأمثلة التي توضح مستوى التركيب في الرياضيات، ومن ضمنها:
تساهم هذه الأمثلة في تعزيز المهارات الإبداعية وتساعد الطلاب على فهم كيفية استخدام المعرفة الرياضية بطرق جديدة.
المستوى السادس: التقييم
يشكل التقييم الفصل النهائي في مستويات بلوم المعرفية، حيث يُعنى بتحديد جودة الحلول المقدمة. يرتكز هذا المستوى على القدرة على إصدار أحكام بشأن الرياضيات بناءً على معايير معينة. يلعب التقييم دورًا محورياً في مساعدتنا على فهم مدى فعالية الحلول وأسباب اختيارها.
تعريف التقييم
التقييم في الرياضيات يعني الحكم على دقة وكفاءة الحلول. يتيح لنا هذا الطرف من المقياس المقارنة بين إجابات مختلفة وتقدير ما إذا كانت الحلول تلبي المعايير المتوقعة. يشمل التقييم:
أمثلة على تقييم الحلول الرياضية
نستطيع من خلال تقييم الحلول الرياضية الاتكاء على أمثلة واضحة. تعكس هذه الأمثلة قدراتنا في إجراء التقييم بشكل فعّال:
استخدام هذه الأمثلة يساعدنا على تطبيق مستوى التقييم بطرق تعزز من فاعلية تعلّم الرياضيات وتُثري تجاربنا الشخصية معها.
Conclusion
نحن نؤمن بأن تطبيق مستويات بلوم المعرفية في الرياضيات يُعد خطوة أساسية نحو تحسين تجربة التعلم. من خلال فهم وتطبيق هذه المستويات يمكننا تعزيز مهارات التفكير النقدي لدى الطلاب وتوفير بيئة تعليمية غنية.
الأمثلة التي استعرضناها تُظهر كيف يمكن للمعلمين والطلاب الاستفادة من هذه المستويات لتطوير الفهم العميق للمفاهيم الرياضية.
نحن نتطلع إلى رؤية المزيد من الابتكارات في طرق التعليم التي تعتمد على هذه الاستراتيجيات، مما يسهم في إعداد جيل قادر على مواجهة التحديات الرياضية بشكل فعّال.